Вопрос:
Я студент, и мне было поручено оптимизировать билинейную интерполяцию изображений, вызывая parallelism из CUDA.
Изображение предоставляется в виде 24-битного формата .bmp. У меня уже есть читатель для .bmp и хранятся пиксели в массиве.
Теперь мне нужно выполнить билинейную интерполяцию в массиве. Я не понимаю математику за ней (даже после прохождения статьи wiki и других результатов Google). Из-за этого я не могу придумать алгоритм.
Есть ли кто-нибудь, кто может мне помочь со ссылкой на существующий билинейный алгоритм интерполяции на одномерном массиве? Или, возможно, ссылку на библиотеку обработки изображений с открытым исходным кодом, которая использует билинейную и бикубическую интерполяцию для масштабирования изображений?
Лучший ответ:
Самый простой способ понять билинейную интерполяцию – понять линейную интерполяцию в 1D.
Эта первая цифра должна дать вам воспоминания о математике средней школы. Учитывая некоторое местоположение a, в котором мы хотим знать f (a), мы берем соседние “известные” значения и устанавливаем между ними линию.
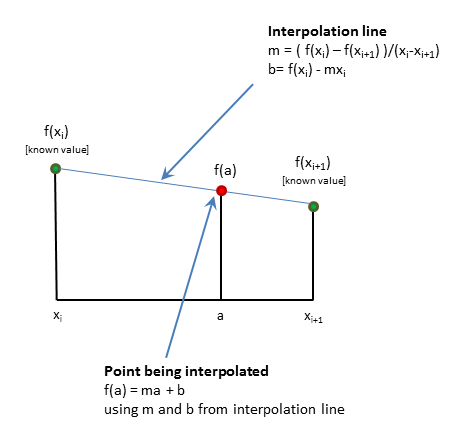

Итак, мы использовали старые уравнения средней школы y = mx + b и y-y1 = m (x-x1). Ничего необычного.
Мы в основном переносим это понятие в двумерное, чтобы получить билинейную интерполяцию. Мы можем атаковать проблему нахождения f (a, b) для любых a, b, выполнив три интерполяции. Внимательно изучите следующий рисунок. Не пугайтесь всех ярлыков. На самом деле это довольно просто.
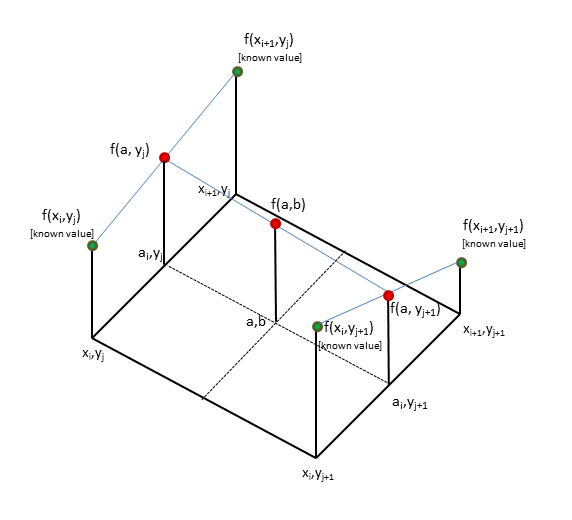

Для билинейной интерполяции мы снова используем соседние точки. Теперь их четыре, поскольку мы находимся в 2D. Трюк состоит в том, чтобы атаковать проблему по одному измерению за раз.
Проецируем наши (a, b) на стороны и сначала вычисляем две (одномерные!) интерполирующие линии.
- f (a, y j), где y j поддерживается постоянным
- f (a, y j + 1), где y j + 1 поддерживается постоянным.
Теперь есть только один последний шаг. Вы берете две рассчитанные вами точки, f (a, y j) и f (a, y j + 1), и установите между ними линию. То, что синий идет слева направо на диаграмме, проходит через f (a, b). Интерполяция по этой последней строке дает окончательный ответ.
Я оставлю математику для 2-D случая для вас. Это не сложно, если вы работаете с диаграммой. И, пройдя через это, вы сами сможете узнать, что происходит.
Одна маленькая заметка, неважно, какие стороны вы выбираете для первых двух интерполяций. Вы могли бы выбрать верх и низ, а затем сделать третью интерполяционную линию между этими двумя. Ответ был бы таким же.
Ответ №1
Когда вы увеличиваете изображение путем масштабирования сторон по интегральному коэффициенту, вы можете рассматривать результат как исходное изображение с дополнительными пикселями, вставленными между исходными пикселями.
Смотрите изображения в ПРИМЕР ИЗОБРАЖЕНИЯ ИЗОБРАЖЕНИЯ.
Формула f(x,y)=… в в этой статье в Википедии дает вам метод вычисления цвета f вставленного пикселя:
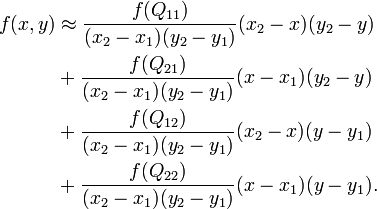
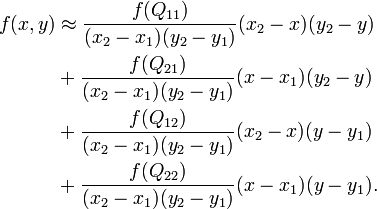
Для каждого вставленного пикселя вы совмещаете цвета четырех исходных пикселей (Q11, Q12, Q21, Q22), окружающих его. Комбинация зависит от расстояния между вставленным пикселем и окружающими исходными пикселями, чем ближе к одному из них, тем ближе их цвета:
Исходные пиксели отображаются красным цветом. Вставляемый пиксель отображается зеленым.
Что идея.
Если вы масштабируете стороны нецелым фактором, формулы все еще сохраняются, но теперь вам нужно пересчитать все пиксельные цвета, поскольку вы не можете просто взять исходные пиксели и просто вставить дополнительные пиксели между ними.
Ответ №2
Не зацикливайтесь на том, что 2D-массивы в C – это действительно 1D-массивы. Это деталь реализации. Математически вам все равно придется думать о 2D-массивах.
Подумайте о линейной интерполяции на 1D-массиве. Вы знаете значение в 0, 1, 2, 3, … Теперь предположим, что я запрашиваю значение в 1.4. Вы дадите мне взвешенное сочетание значений в 1 и 2: (1 — 0.4)*A[1] + 0.4*A[2]. Просто, правильно?
Теперь вам нужно перейти к 2D. Нет проблем. 2D-интерполяция может быть разложена на две одномерные интерполяции по оси x, а затем по оси y. Скажем, вы хотите (1.4, 2.8). Получите 1D-интерполяцию между (1, 2)<->(2,2) и (1,3)<->(2,3). Это ваш шаг оси x. Теперь 1D интерполирует между ними с соответствующими весами для y = 2.8.
Это должно быть простым для массового параллелизма. Просто вычислите каждый интерполированный пиксель отдельно. При использовании доступа к исходному изображению доступ к общей памяти вы будете делать только чтение, поэтому никаких проблем с синхронизацией.

