Вопрос:
Я пытаюсь оценить/проверить, насколько хорошо мои данные соответствуют определенному дистрибутиву.
Есть несколько вопросов об этом, и мне сказали использовать либо scipy.stats.kstest либо scipy.stats.ks_2samp. Это кажется простым, дайте ему: (A) данные; (2) распределение; и (3) параметры подгонки. Единственная проблема – мои результаты не имеют никакого смысла? Я хочу проверить “доброту” моих данных и соответствовать различным дистрибутивам, но из результата kstest я не знаю, смогу ли я это сделать?
Хорошие тесты пригодности в SciPy
“[SciPy] содержит KS”
Используя модуль stats.kstest от Scipy для тестирования пригодности
“Первое значение – это тестовая статистика, а второе значение – p-значение. Если значение p меньше 95 (для уровня значимости 5%), это означает, что вы не можете отклонить Null-Hypothese, что два выборочные распределения идентичны “.
Это просто показывает, как соответствовать: фиктивные распределения, добротность приставки, значение p. Можно ли это сделать с помощью Scipy (Python)?
np.random.seed(2) # Sample from a normal distribution w/ mu: -50 and sigma=1 x = np.random.normal(loc=-50, scale=1, size=100) x #array([-50.41675785, -50.05626683, -52.1361961 , -48.35972919, # -51.79343559, -50.84174737, -49.49711858, -51.24528809, # -51.05795222, -50.90900761, -49.44854596, -47.70779199, # … # -50.46200535, -49.64911151, -49.61813377, -49.43372456, # -49.79579202, -48.59330376, -51.7379595 , -48.95917605, # -49.61952803, -50.21713527, -48.8264685 , -52.34360319]) # Try against a Gamma Distribution distribution = «gamma» distr = getattr(stats, distribution) params = distr.fit(x) stats.kstest(x,distribution,args=params) KstestResult(statistic=0.078494356486987549, pvalue=0.55408436218441004)
P_value pvalue=0.55408436218441004 говорит, что normal и gamma выборка происходят из одних и тех же решеток?
Я думал, что гамма-распределения должны содержать положительные значения? https://en.wikipedia.org/wiki/Gamma_distribution
Теперь против нормального распространения:
# Try against a Normal Distribution distribution = «norm» distr = getattr(stats, distribution) params = distr.fit(x) stats.kstest(x,distribution,args=params) KstestResult(statistic=0.070447707170256002, pvalue=0.70801104133244541)
В соответствии с этим, если бы я взял наименьшее значение p_value, то я бы сделал вывод, что мои данные поступают из gamma распределения, хотя они все отрицательные значения?
np.random.seed(0) distr = getattr(stats, «norm») x = distr.rvs(loc=0, scale=1, size=50) params = distr.fit(x) stats.kstest(x,»norm»,args=params, N=1000) KstestResult(statistic=0.058435890774587329, pvalue=0.99558592119926814)
Это означает, что на уровне 5% значимости я могу отклонить нулевую гипотезу о том, что распределения идентичны. Поэтому я пришел к выводу, что они разные, но, очевидно, нет? Я интерпретирую это неправильно? Если я сделаю это односторонней, это сделает так, что чем больше значение, тем больше вероятность того, что они из одного и того же дистрибутива?
Лучший ответ:
Итак, нулевая гипотеза для теста KT заключается в том, что распределения одинаковы. Таким образом, чем ниже значение p, тем больше статистических данных, которые вы должны отклонить от нулевой гипотезы, и заключить, что распределения различны. Тест только на самом деле позволяет говорить о вашей уверенности в том, что дистрибутивы разные, а не то же самое, поскольку тест предназначен для поиска альфы, вероятность ошибки типа I.
Кроме того, я уверен, что тест KT действителен только в том случае, если у вас есть полностью определенное распределение в виду заранее. Здесь вы просто подходите к гамма-распределению на некоторые данные, поэтому, конечно, не удивительно, что тест дал высокое значение p (т.е. Вы не можете отклонить нулевую гипотезу о том, что распределения одинаковы).
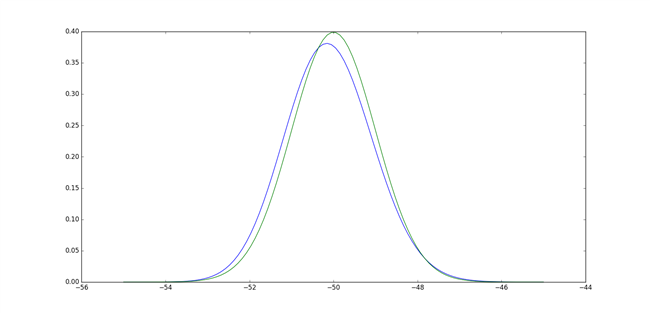
Реальный быстро, вот pdf файл Gamma, который вы подходите (в синем) к pdf-каналу обычного распределения, с которым вы выбрали (зеленым):
In [13]: paramsd = dict(zip((‘shape’,’loc’,’scale’),params)) In [14]: a = paramsd[‘shape’] In [15]: del paramsd[‘shape’] In [16]: paramsd Out[16]: {‘loc’: -71.588039241913037, ‘scale’: 0.051114096301755507} In [17]: X = np.linspace(-55, -45, 100) In [18]: plt.plot(X, stats.gamma.pdf(X,a,**paramsd)) Out[18]: [<matplotlib.lines.Line2D at 0x7ff820f21d68>]
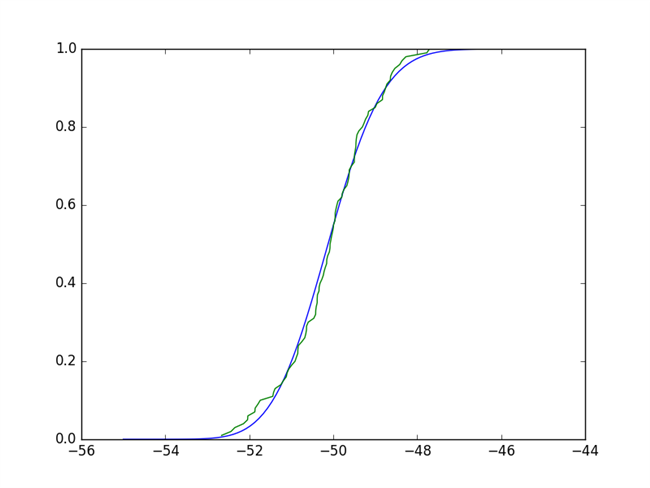
Это должно быть очевидно, что они не очень разные. Действительно, тест сравнивает эмпирический CDF (ECDF) и CDF вашего кандидата-кандидата (что опять же вы получили от подгонки ваших данных к этому распределению), а статистическая статистика – максимальная разница. Заимствование реализации ECDF здесь, мы можем видеть, что любая такая максимальная разница будет невелика, и тест будет явно не отвергнуть нулевую гипотезу:
In [32]: def ecdf(x): …..: xs = np.sort(x) …..: ys = np.arange(1, len(xs)+1)/float(len(xs)) …..: return xs, ys …..: In [33]: plt.plot(X, stats.gamma.cdf(X,a,**paramsd)) Out[33]: [<matplotlib.lines.Line2D at 0x7ff805223a20>] In [34]: plt.plot(*ecdf(x)) Out[34]: [<matplotlib.lines.Line2D at 0x7ff80524c208>]